二分查找

2017-07-31 | 阅读：11次

二分查找主要是解决在“一堆数中找出指定的数”这类问题。而想要应用二分查找，这“一堆数”必须满足以下特征：

存储在数列中
有序排列所以如果是用链表存储的，就无法再其上应用二分查找了

二分查找的基本实现

非递归算法：

public static int binary_search(int arr[],int n ,int key){  
    int mid;  
    int low = 0,high = n-1;  
    while(low <= high){  
        mid =  (high + low)/2;   //中间元素，防止溢出  
        if(key == arr[mid]) return mid;//找到时返回  
        else if(key > arr[mid]){  
            low = mid + 1;//在更高的区间搜索  
        }else{  
            high = mid - 1;//在更低的区间搜索  
        }  
    }  
    return -1;//没有找到元素，返回-1  
}  

递归算法：

public static int BinSearch(int Array[],int low,int high,int key)  
{  
    if (low<=high)  
    {  
        int mid = (low+high)/2;  
        if(key == Array[mid])  
            return mid;  
        else if(key<Array[mid])  
            //移动low和high  
            return BinSearch(Array,low,mid-1,key);  
        else if(key>Array[mid])  
            return BinSearch(Array,mid+1,high,key);  
    }  
    else  
        return -1;  
}  

用二分查找寻边界值

在有序数组中找到“正好大于（小于）目标数”的数举例：

int array = {2, 3, 5, 7, 11, 13, 17};
int target = 7;

那么上界值应该是11，因为它“刚刚好”大于7；下届值则是5，因为它“刚刚好”小于7。

寻上界：

public static int BSearchUpperBound(int array[], int low, int high, int target)
{
    //Array is empty or target is larger than any every element in array 
    if(low > high || target >= array[high]) return -1;
    
    int mid = (low + high) / 2;
    while (high > low)
    {
        if (array[mid] > target)
            high = mid;
        else
            low = mid + 1;
        
        mid = (low + high) / 2;
    }

    return mid;
}

寻下界：

public static int BSearchUpperBound(int array[], int low, int high, int target)
{
    //Array is empty or target is larger than any every element in array 
    if(low > high || target >= array[high]) return -1;
    
    int mid = (low + high) / 2;
    while (high > low)
    {
        if (array[mid] > target)
            high = mid;
        else
            low = mid + 1;
        
        mid = (low + high) / 2;
    }

    return mid;
}

旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增的排序的数组的一个旋转，输出旋转数组的最小元素。例如输入{1,2,3,4,5}的一个旋转为{3,4,5,1,2}，该数组的最小值为1。

可以把有序数组经过旋转以后被分割为两段有序的数组，比如此处被分为{3,4,5}{1,2}这样两个数组，并且前半段数组中的数字肯定大于等于后半段的数组。我们找中间元素，让其跟元素首元素比较，如果大于首元素，则中间元素属于前半段有序数组，如果小于尾元素，那么中间元素就是后半段的元素。

这里我们设定两个指针start和end分别指向数组的首尾元素，然后当start指向前半段最后一个元素，end指向后半段第一个元素，这是程序就找到了数组中的最小元素，就是end指向的那个数，程序的出口就是 end-start==1。

实现代码：

public static int SearchInRotatedSortedArray(int array[], int low, int high, int target) 
{
    while(low <= high)
    {
        int mid = (low + high) / 2;
        if (target < array[mid])
            if (array[mid] < array[high])
                high = mid - 1;  
            else    
                if(target < array[low])
                    low = mid + 1;
                else
                    high = mid - 1;

        else if(array[mid] < target)
            if (array[low] < array[mid])
                low = mid + 1; 
            else
               if (array[high] < target)
                    high = mid - 1;
                else
                    low = mid + 1;
        else //if(array[mid] == target)
            return mid;
    }

    return -1;
}

有序矩阵中二分查找

如果矩阵中每一行元素都是有序的，而且下一行的元素都大于等于上一行元素，这种情况下把矩阵抽象成一个一维数组即可用普通的二分完成。

如果矩阵元素满足每一行中右边的比左边的大，每一列下一个比上一个大，解法如下：

解法一是从矩阵的右上角元素开始作比较，如果小于，则向左滑动；如果大于则向下滑动，从而可以减小搜索的空间而解决一个子问题。时间复杂度最坏情况下是O(m+n)。

实现代码：

public class SearchInSortedMatrix
{
    public static boolean searchMatrix(int[][] matrix, int target)
    {
        int m = matrix.length;
        int n = matrix[0].length;
        int low = 0;
        int high = m*n - 1;
        while(low <= high)
        {
            int mid = (low + high)/2;
            int row = mid / n;
            int column = mid % n;
            if(matrix[row][column] == target)
            {
                return true;
            }
            else if(matrix[row][column] < target)
            {
                low = mid + 1;
            }
            else
            {
                high = mid - 1;
            }
        }
        return false;
    }
}

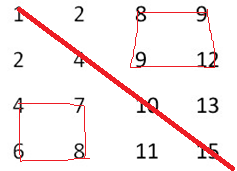
解法二：以查找数字6为例，因为矩阵的行和列都是递增的，所以整个矩阵的对角线上的数字也是递增的，故我们可以在对角线上进行二分查找，如果要找的数是6介于对角线上相邻的两个数4、10，可以排除掉左上和右下的两个矩形，而在左下和右上的两个矩形继续递归查找，如下图所示：

实现代码：

public  boolean searchMatrix2(int[][] matrix, int target)
{
    int m = matrix.length;
    int n = matrix[0].length;
    return helper(matrix, 0, m-1, 0, n-1, target);
}
public boolean helper(int[][] matrix, int rowStart, int rowEnd, int colStart, int colEnd, int target)
{
    int rm = (rowStart + rowEnd)/2;
    int cm = (colStart + colEnd)/2;
    if(rowStart > rowEnd || colStart > colEnd)
    {
        return false;
    }
    if(matrix[rm][cm] == target)
    {
        return true;
    }
    else if(matrix[rm][cm] > target)
    {
        return helper(matrix, rowStart, rm - 1, colStart, cm - 1, target)
            || helper(matrix, rm, rowEnd, colStart, cm - 1, target)
            || helper(matrix, rowStart, rm - 1, cm, colEnd, target);
    }
    else
    {
        return helper(matrix, rm + 1, rowEnd, cm + 1, colEnd, target)
            || helper(matrix, rm + 1, rowEnd, colStart, cm, target)
            || helper(matrix, rowStart, rm, cm + 1, colEnd, target);
                
    }
}
 
//从右上角元素进行查找
public boolean searchMatrix3(int[][] matrix, int target)
{
    int m = matrix.length;
    int n = matrix[0].length;
    int low = 0;
    int high = m*n - 1;
    while(low <= high)
    {
        int mid = (low + high)/2;
        int row = mid / n;
        int column = mid % n;
        if(matrix[row][column] == target)
        {
            return true;
        }
        else if(matrix[row][column] < target)
        {
            low = mid + 1;
        }
        else
        {
            high = mid - 1;
        }
    }
    return false;
}

二分查找的缺陷

二分查找法是十分高效的算法，不过它的缺陷却也是那么明显的。就在它的限定之上：

必须有序，很难保证数组都是有序的。可以在构建数组的时候进行排序
必须是数组

数组读取效率是O(1)，可是它的插入和删除某个元素的效率却是O(n)。因而导致构建有序数组变成低效的事情。

解决这些缺陷问题更好的方法应该是使用二叉查找树了，最好是自平衡二叉查找树了，既能高效的（O(n log n)）构建有序元素集合，又能如同二分查找法一样快速（O(log n)）的搜寻目标数。

打赏一个呗

感谢您的支持，我会继续努力的!

扫码打赏，你说多少就多少

打开支付宝扫一扫，即可进行扫码打赏哦